Integral Substitusi

Dalam pengintegralan kita sering kesulitan karena masalah fungsi, misalkan adanya pangkat yang tinggi, bentuk akar, serta fungsi-fungi trigonometri. Untuk itu maka digunakan penggantian, atau disebut substitusi. karena itulah pada langkah ini dilakukan pemisalan.

Contoh :


dari bentuk ini yang kita lakukan adalah dengan memisalkan
misal y = 3x - 4
maka

sehingga

Jadi, bentuk integral menjadi




contoh 2

misal :
y = x² + 6
maka

sehingga

Jadi :





materi sebelumnya

materi berikutnya

Turunan 2

contoh 3
maka
sehingga :




contoh 3
maka








materi sebelumnya
materi berikutnya

Integral Tak Tentu 2

Soal-soal Integral tak tentu


















materi sebelumnya
materi berikutnya

Turunan

Turunan seringkali didefinisikan dengan

Untuk lebih jelanya, tentukanlah turunandari fungsi-fungsi berikut :
1. f(x) = x²
2. f(x) = x³




Jawab :
untuk nomor 1 :
f(x) = x² maka f(x) = (x+ h) ² sehingga






dengan demikian turunan pertama dari f(x) = x² adalah f'(x) = 2x

Untuk nomor 2 bisa kita selesaikan sebagai berikut :
f(x) = x³ maka f(x) = (x+ h) ³ sehingga






f'(x) = 3x²+0+0 = 3x²
Jadi, jika f(x) = x³ maka f'(x) = 3x²

Dengan demikian kita bisa mengambil kesimpulah bahwa
Jika f(x) = xⁿ maka f'(x) = nx^n-1

materi berikutnya (pembahasan nomor 3 dan 4)

Integral Tak Tentu

Integral sering desebut dengan anti turunan.Hal ini karena memang integral diperoleh dengan membalik turunan. Perhatikan hitungan berikut

y = x⁵ maka y' = 5x⁴
y = x⁵ + 2 maka y' = 5x⁴
y = x⁵ + 100 maka y' = 5x⁴
y = x⁵ - 100 maka y' = 5x⁴

Jika bentuk ini dibalik dari kanan ke kiri maka diperoleh

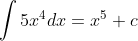
dengan c adalah konstanta yang besarnya tidak tentu. Sesuai dengan turunan di atas mungkin anda akan berfikir bahwa nilai c adalah 0, 2, 100, atau -100. Ya, ini tidak salah. karena banyaknya kemungkinan selain kemungkinan di atas maka akhirnya disepakati dengan memakai c saja.

Dari sini bisa diambil kesimpulan bahwa


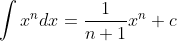
dengan ketentuan
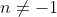
kenapa? Karena jika n = -1 maka penyebut di ruas kanan menjadi nol

Untuk n = -1 maka akan menjadi

dengan ln melambangkan logaritma natural.
ln x = ^elog x
dengan e = bilangan natural
Besarnya e adalah
e = 2,71828 .......
yang merupakan bilangan natural

Sifat-sifat integral tak tentu :




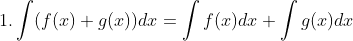
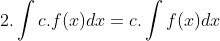
untuk lebih jelasnya, perhatikan contoh soal berikut