MATEMATIKA INDONESIA: September 2012

Sabtu, 29 September 2012

Sudut Istimewa Dalam Trigonometri

Materi ini adalah lanjutan dari fungsi trigonometri.
Dalam trigonometri, ada sudut-sudut yang dikatakan sudut istimewa. Sudut Istimewa dalam trigonometri tersebut adalah 0^o, 30^o, 45^o, 60^o dan 90^o
Marilah kita hitung nilai sinus, cosinus, dan tangen dari sudut istimewa ini

Untuk sudut 45^o

Segitiga siku-siku yang memiliki sudut 45^o pastila memiliki sudut-sudut 45^o, 90^o dan 45^o, sehingga merupakan segitiga siku-siku sama kaki. Jadi kedua sisi siku-sikunya pasti sama, dan kita pilih besarnya 1. Dari sini kita bisa memperoleh sisi miring sebesar
$\sqrt{1^{2}+1^{2}}=\sqrt{2}$

Dari gambar bisa disimpulkan
$\sin\alpha =\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1}{2}\sqrt{2}$

$\cos\alpha =\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1}{2}\sqrt{2}$

$\tan\alpha =\frac{1}{1}=1$

Untuk sudut 60^o

Pada segitiga sama sisi, ketiga sudutnya masing-masing adalah 60^o. Ketiga sisinya sama dan kita pilih besarnya 2. Segitiga ini sekarang kita belah 2 sama secara vertikal, sehingga alasnya terbagi 2 sama, masing-masing panjangnya 1. Dari sini kita peroleh dua buah segitiga siku-siku. Dengan memakai rumus pythagoras kita bisa memperoleh tinggi segitiga, yaitu
$\sqrt{2^{2}-1^{2}}=\sqrt{4-1}=\sqrt{3}$

Dari segitiga siku-siku sebelah kiri, kita bisa menentukan sin 60^o, cos 60^o, dan tan 60^o yaitu :
$\sin60^{o}=\frac{\sqrt{3}}{2}=\frac{1}{2}\sqrt{3}$

$\cos60^{o}=\frac{1}{2}$

$\tan 60^{o}=\frac{\sqrt{3}}{1}=\sqrt{3}$

Untuk sudut 30^o
Dari segitiga sama sisi di atas, sekarang kita ambil bagian kanan (warna kuning) dan kita putar 90^o berlawanan arah jarum jam, sehingga kita peroleh sebagai berikut :

Dari gambar kita bisa memperoleh nilai sinus 30^o, cos 30^o dan tan 30^o
$\sin 30^{o}=\frac{1}{2}$

$\cos 30^{o}=\frac{\sqrt{3}}{2}=\frac{1}{2}\sqrt{3}$

$\tan 30^{o}=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$

Untuk mempermudah mengingat hasil pembuktian ini maka dudut-sudut istimewa ini kita susun dalam tabel trigonometri.

Kamis, 27 September 2012

Persamaan Garis Singgung 2

Persamaan garis singgung yang diketahui gradiennya.

Pada bagian ini kita mulai dari contoh 6 dan seterusnya. Contoh-contoh sebelumnya, silakan di klik di sini

Contoh 6 :
Tentukan persamaan garis singgung pada kurva y = x⁴ - 100x yang bergradien 8

Jawab :
m = 8
y' = 8
4x³ - 100 = 8
4x³ = 108
x³ = 27
x = 3
y = x⁴ - 100x = 81 - 300 = - 219
Persamaan garisnya adalah :
y - y₁ = m(x - x₁)
y + 219 = 8(x - 3)
y + 219 = 8x - 24
y = 8x - 243

Contoh 7 :
Persamaan garis singgung pada kurva y = 3x⁴ - 20 yang sejajar dengan garis y = 12x + 8 adalah

Jawab :
y = 3x⁴ - 20
y' = 12x³
Persamaan garis yang sejajar dengan garis singgung adalah
y = 12x + 8
maka gradien garis ini adalah m₁ = 12
Karena sejajar maka gradiennya sama sehingga gradien garis singgung (m₂) adalah
m₂ = m₁ = 12
gradien garis singgung ini sama dengan turunan kurva sehingga
y' = 12
12x³ = 12
x³ = 1
x = 1
maka y = 3x⁴ - 20 = 3 - 20 = - 17
Persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)
y + 17 = 12(x - 1)
y + 17 = 12x - 12
y = 12x - 29

Contoh 8 :
Garis yang menyinggung kurva y = 12 - x⁴ dan tegak lurus dengan x - 32y = 48 mempunyai persamaan ....

Jawab :
y = 12 - x⁴
y' = - 4x³

Persamaan garis dari soal :
x - 32y = 48
32y = x - 48
$y=\frac{1}{32}x-2$
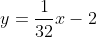
Garis ini memiliki gradien
$m_{1}=\frac{1}{32}$

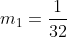
Karena garis singgungnya tegak lurus dengan garis ini maka
m₁.m₂ = -1
$\frac{1}{32}m_{2}=-1$
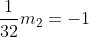
m₂= -32
m₂ ini adalah gradien garis singgung, sehingga sama dengan turunan
y' = -32
- 4x³ = -32
x³ = 8
x = 2
y = 12 - x⁴ = 12-2⁴ = -4
Persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)
y + 4 = -32(x - 2)
y + 4 = -32x + 64
y = -32x + 60

Contoh 9 :
Tentukan persamaan garis singgung pada kurva y = 1/x yang sejajar dengan garis x + 4y = 20 adalah ...

Jawab :
$y=-\frac{1}{x}=x^{-1}$
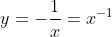
maka
$m=y'=-x^{-2}=-\frac{1}{x^{2}}$

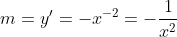
Persamaan garis dari soal adalah
4y = -x + 20
$y=-\frac{1}{4}x+5$
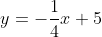
gradien garis ini adalah
$m_{1}=-\frac{1}{4}$
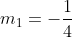
Syarat 2 garis sejajar adalah gradiennya sama sehingga gradien garis singgung (m₂) adalah
$m_{2}=m_{1}=-\frac{1}{4}$
karena gradien garis singgung sama dengan turunan maka
$y'=-\frac{1}{4}$
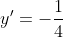
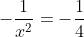
$-\frac{1}{x^{2}}=-\frac{1}{4}$

x² = 4

$x=\pm 2$

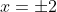Untuk x = 2 maka diperoleh :
y = 1/x = 1/2
maka persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)
$y-\frac{1}{2}=-\frac{1}{4}(x-2)$
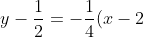Jika kedua ruas dikali 4 maka diperoleh :
4y - 2 = - x + 2
x + 4y - 4 = 0

Untuk x = - 2 maka diperoleh
y = 1/x = - 1/2
maka persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)

$y+\frac{1}{2}=-\frac{1}{4}(x+2)$

Jika kedua ruas dikali 4 maka
4y + 2 = -x - 2
x + 4y + 4 = 0

Contoh 10 :
Persamamaan garis singgung pada kurva y = x³ + 10 yang tegak lurus dengan x + 27y = 81 adalah ....

Jawab :
y = x³ + 10
y' = 3x²
Persamaan garis dari soal adalah
x + 27y = 81
27y = -x + 81
$y=-\frac{1}{27}x+3$
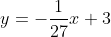
gradien garis ini adalah
$m_{1}=-\frac{1}{27}$
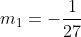
Karena saling tegak lurus maka berlaku
m₁.m₂ = -1
$-\frac{1}{27}m_{2}=-1$
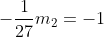
m₂ = 27
Gradien garis singgung ini sama dengan turunan fungsi , sehingga
y' = 27
3x² = 27
x² = 9
x = 3 atau x = -3

Untuk x = 3 maka
y = x³ + 10 = 27 + 10 = 37
Persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)
y - 37 = 27(x - 3)
y - 37 = 27x - 81
y = 27x - 44

Untuk x = -3 maka
y = x³ + 10 = -27 + 10 = -17
Persamaan garis singgungnya adalah
y - y₁ = m(x - x₁)
y + 17 = 27(x + 3)
y + 17 = 27x + 81
y = 27x + 64

Soal Belah Ketupat Dan Jawabannya

Soal Belah Ketupat Dan Jawabannya
Berikut ini adalah jawaban dari soal-soal belah ketupat. Untuk melihat soalnya, silakan di klik di sini

1. sisi = 7 cm , maka keliling = 4xsisi = 4x7 = 28 cm
2. d₁ = 10 cm, d₂ = 6 cm
Luas belah ketupat = 0,5 x d₁ x d₂ = 0,5 x 10 x 6 = 30 cm²

3. d₁ = 8 cm
Luas = 48 cm²
0,5 x d₁ x d₂ = 48
0,5 x 8 x d₂ = 48
d₂ =12 cm

Sebuah belah ketupat panjang salah satu diagonalnya adalah 12 cm dan panjang sisinya
adalah 10 cm. Luas belah ketupat sama dengan

4. d₁ = 12 ===> OB = 0,5x d₁ = 0,5 x 12 = 6
s = 10 ===> AB = 10

$OA=\sqrt{AB^{2}-OB^{2}}=\sqrt{100-36}=\sqrt{64}=8$
d₂ = 2xOA = 2 x 8 =16 cm
Luas belah ketupat = 0,5 x d₁ x d₂ = 0,5x12x16 = 96 cm2

5. K = 52 cm ==> s = 0,25xK = 0,25x52 = 13 cm ===> AB = 13 cm
d₁ = 10 cm ===> OB = 5 cm

$OA=\sqrt{AB^{2}-OB^{2}}=\sqrt{169-25}=\sqrt{144}=12$
d₂ = 2 x OA = 2 x 12 = 24 cm
Luas belah ketupat = 0,5 x d₁ x d₂ = 0,5x 10 x 24 = 120 cm²

6. d₁ = 30 cm ===> AC = 30 cm ===> OA = 0,5 x AC = 0,5 x 30 = 15 cm
L = 240
0,5 x d₁ x d₂ = 240
0,5 x 30 x d₂ = 240
15 x d₂ = 240
d₂ =16 ===> AB = 16 ===> OB = 8 cm

$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{225+64}=\sqrt{289}=17$

s = AB = 17 cm
Keliling belah ketupat = 4 x s = 4 x 17 = 68 cm

7. K = 40 ===> s = 0,25 x K = 0,25 x 40 = 10 cm
L = 96 cm²
0,5 x d₁ x d₂ =96

0,5 2xOA x 2 x OB = 96
2xOA x OB = 96
OA x OB =48

$OB=\frac{48}{OA}$
OA² + OB² = s²

$OA^{2}+\left ( \frac{48}{OA} \right )^{2}=10^{2}$

$OA^{2}+\frac{2304}{OA^{2}}=100$

OA⁴ + 2304 = 100OA²
OA⁴ - 100OA² + 2304 = OA²
(OA² - 36)(OA² - 64) = 0
OA² = 36 atau OA² = 64
Misalkan kita pilih saja OA² = 64 maka OA = 8

$OB=\frac{48}{OA}=\frac{48}{8}=6$

d₁ = 2 x OA = 2 x 8 = 16 cm
d₂ = 2 x OB = 2 x 6 = 12 cm

8. d₁ = 8 cm ===> OB = 0,5 x d₁ = 0,5 x 8 = 4 cm

$\frac{OB}{OA}=\tan 30^{o}$

$\frac{4}{OA}=\frac{1}{\sqrt{3}}$
$OA=4\sqrt{3}$

$d_{2}=2\times OA=8\sqrt{3}$

$L=\frac{1}{2}d_{1}\times d_{2}=\frac{1}{2}\times 8\times 8\sqrt{3}=\begin{matrix} 32\sqrt{3} & cm^{2} \end{matrix}$

Rabu, 26 September 2012

Turunan Logaritma Natural 2

Bab Turunan logaritma natural ini merupakan lanjutan dari bilangan natural. Berikut ini saya berikan contoh-contoh turunan dari logaritma natural.
Aturan rantai bisa dipakai pada logaritma natural ini, jadi

$y=\ln f(x) \rightarrow y' = \frac{1}{f(x)}.f'(x)$

Contoh 1 :
Tentukan turunan pertama dari y = ln (8x +1)

Jawab :

$y' = \frac{1}{8x+1}.8=\frac{8}{8x+1}$

Contoh 2 :
Tentukan turunan pertama dari y = ln 9x adalah ....

Jawab :
Cara I :
$y' = \frac{1}{9x}.9=\frac{1}{x}$

Cara II
y = ln 9x = ln 9 + ln x
maka
$y' = 0+\frac{1}{x}=\frac{1}{x}$
(ln 9 adalah konstanta, jadi turunannya = 0)

Contoh 3 :
Turunan pertama dari y = ln sin x adalah ...

Jawab :
$y' = \frac{1}{\sin x}.cosx=\cot x$

Contoh 4 :
Turunan pertama dari y = ln cos x adalah ...

Jawab :
$y' = \frac{1}{\cos x}.(-\sin x)=-\tan x$

Contoh 5 :
Jika y = ln sec x maka dy/dx = ....

Jawab :
$\frac{dy}{dx} = \frac{1}{\sec x}.\sec x.\tan x =\tan x$

Contoh 6 :

Jika y = ln csc x maka dy/dx = ...

Jawab :
$\frac{dy}{dx} = \frac{1}{\csc x}.(-\csc x).\cot x =-\cot x$

Contoh 7 :
Jika f(x) = ln (sec x + tan x) maka f '(x) = ...

Jawab :
$f'(x) = \frac{1}{\sec x+ \tan x}.(\sec x.\tan x +\sec^{2}x)$

$f'(x) = =\frac{\sec x(\sec x+ \tan x)}{\sec x+ \tan x}=\sec x$

Contoh 8 :
Jika f(x) = ln (csc x + cot x) maka df/dx = ...

Jawab :

$\frac{df}{dx} = \frac{1}{\csc x+ \cot x}.(-\csc x.\cot x -\csc^{2}x)$

$\frac{df}{dx} = \frac{-\csc x(\csc x+ \cot x)}{\csc x+ \cot x}=-\csc x$

Contoh 9 :
Tentukan turunan pertama dari
$f(x)=\ln\left ( tan\frac{1}{2}x \right )$

Jawab :
$f'(x)=\frac{1}{tan\left ( \frac{1}{2} x\right )}.\sec^{2}\left ( \frac{1}{2}x \right ).\frac{1}{2}=\frac{cos\left ( \frac{1}{2}x \right )}{\sin \frac{1}{2}x}.\frac{1}{\cos^{2}x}.\frac{1}{2}$

$f'(x)=\frac{1}{2\sin \left ( \frac{1}{2}x \right )\cos \left ( \frac{1}{2}x \right )}=\frac{1}{\sin x}=\csc x$

Contoh 10 :
Tentukan turunan pertama dari
$y=\ln\left ( \cot \frac{1}{2}x\right )$

Jawab :
$y'=\frac{1}{cot\frac{1}{2}x}.\left ( -csc^{2}\frac{1}{2}x \right ).\frac{1}{2}=-\frac{sin\frac{1}{2}x}{\cos \frac{1}{2}x}.\frac{1}{\sin ^{2}\frac{1}{2}x}.\frac{1}{2}$
$y'=-\frac{1}{2\sin \frac{1}{2}x\cos \frac{1}{2}x}=-\frac{1}{\sin x}=-\csc x$

Contoh 11 :
Turunan pertama dari
$f(x)=ln\left ( x+\sqrt{x^{2}+1} \right )$
adalah ...

Jawab :
$f'(x)=\frac{1}{x+\sqrt{x^{2}+1}}\left ( 1+\frac{1}{2}\left ( x^{2}+1 \right )^{-\frac{1}{2}.}.2x \right )$

$f'(x)=\frac{1}{x+\sqrt{x^{2}+1}}\left ( 1+\frac{x}{\sqrt{x^{2}+1}} \right )=\frac{1}{x+\sqrt{x^{2}+1}}\left ( \frac{\sqrt{x^{2}+1}+x}{\sqrt{x^{2}+1}} \right )$

$f'(x)=\frac{1}{\sqrt{x^{2}+1}}$